题目描述
给出一棵树,要求你为树上的结点标上权值,权值可以是任意的正整数
唯一的限制条件是相邻的两个结点不能标上相同的权值,要求一种方案,使得整棵树的总价值最小。
输入格式
先给出一个数字 $N$ ,代表树上有 $N$ 个点, $N<=10000$ 。
下面 $N-1$ 行,代表两个点相连。
输出格式
最小的总权值。
样例 #1
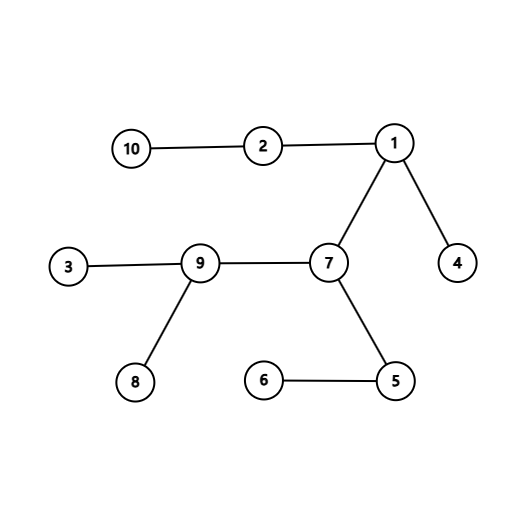
样例输入 #1
10
7 5
1 2
1 7
8 9
4 1
9 7
5 6
10 2
9 3
样例输出 #1
14
提示
本题已经添加数据,但考虑到题目年代较为久远(毕竟是2003年的BOI了)以及洛谷神速评测姬,将此题时限修改为500ms。
题解
这题并不是双颜色染色问题那么简单,不妨考虑如下结构:
$Tree:\ 一个节点(点权为\ 2)有三个子节点(点权都为\ 1)$
若交换父亲与儿子的点权,则增量为 $2$ : $(1+2+2+2)-(2+1+1+1)=2$ ;
考虑父亲的父亲的变化(考虑父亲有多个这样的子树限制):$3\Rightarrow 2$ ,增量为 $-1$ ;
上述总的增量为正,其他子树同理可以变换,因此最大值的最小值随着 $n$ 的变化而变化,大致为 $m=log2(n)$ (未证明)。
于是问题转变为了多颜色染色问题,颜色总数不超过 $m$ 。