题目描述
一棵二叉树可以按照如下规则表示成一个由 $0$、$1$、$2$ 组成的字符序列,我们称之为“二叉树序列 $S$”:
\[S= \begin{cases} 0& \text表示该树没有子节点\\ 1S_1& 表示该树有一个节点,S_1 为其子树的二叉树序列\\ 2S_1S_2& 表示该树由两个子节点,S_1 和 S_2 分别表示其两个子树的二叉树序列 \end{cases}\]例如,下图所表示的二叉树可以用二叉树序列 $S=\texttt{21200110}$ 来表示。
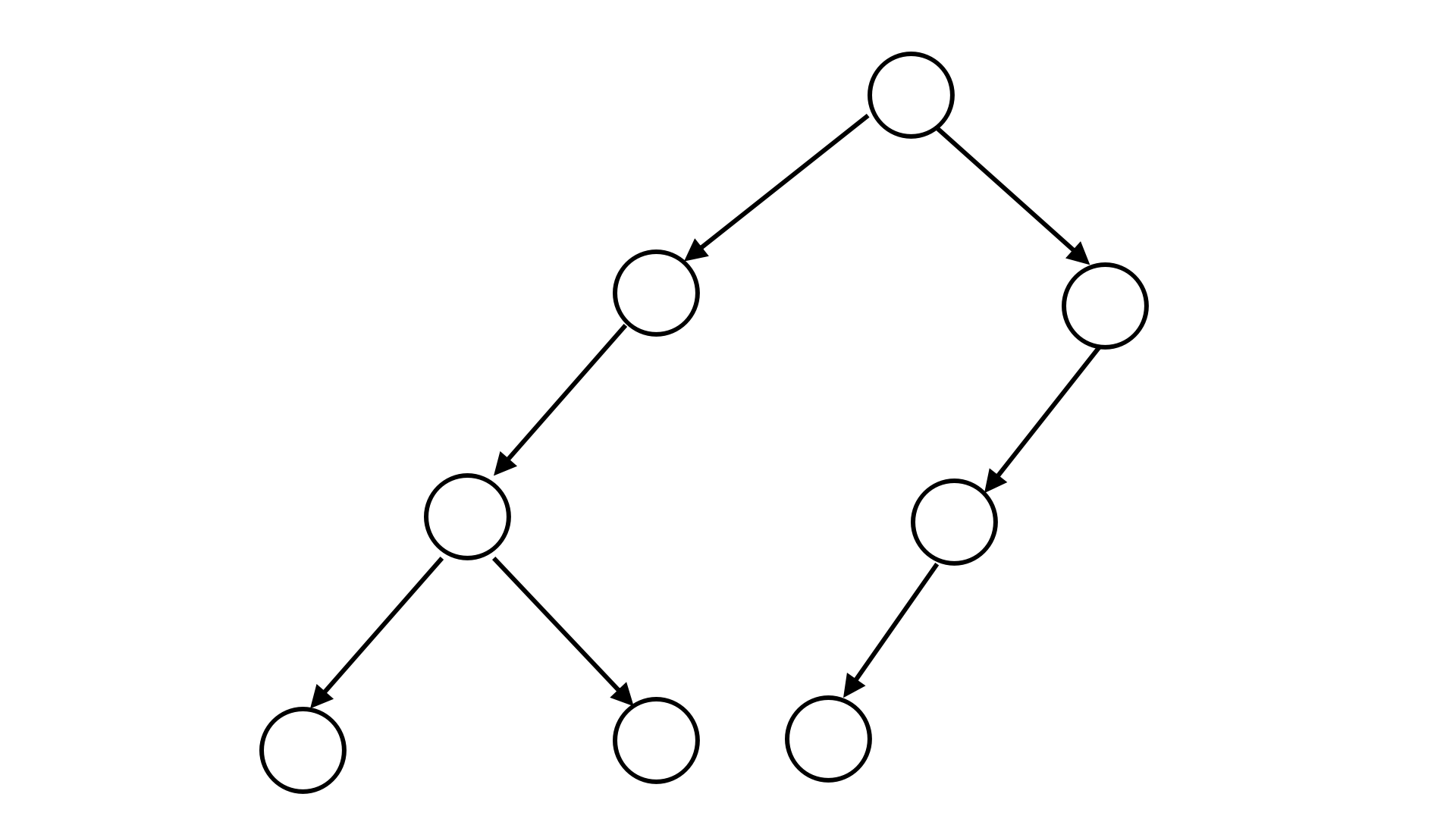
你的任务是要对一棵二叉树的节点进行染色。每个节点可以被染成红色、绿色或蓝色。并且,一个节点与其子节点的颜色必须不同,如果该节点有两个子节点,那么这两个子节点的颜色也必须不同。给定一颗二叉树的二叉树序列,请求出这棵树中最多和最少有多少个点能够被染成绿色。
输入格式
输入只有一行一个字符串 $s$,表示二叉树序列。
输出格式
输出只有一行,包含两个数,依次表示最多和最少有多少个点能够被染成绿色。
样例 #1
样例输入 #1
1122002010
样例输出 #1
5 2
提示
数据规模与约定
| 对于全部的测试点,保证 $1 \leq | s | \leq 5 \times 10^5$,$s$ 中只含字符 0 1 2。 |
题解
建树
由字符串可以递归建树,每个节点做如下规定:
struct node {
int cnt = 0; // 儿子个数
int son[2] = { 0,0 };
} p[N];
状态转移
使用 $dp[u][2]$ 表示节点 $u$ 处选择绿色(1)或不选绿色(0)的情况下,以 $u$ 为根节点的子树中绿色出现的最值。状态转移如下:
- $dp[u][0]$ :儿子不能全选绿色或全不选绿色(只有三色),则 $dp[u][0] = \max(dp[v_1][0]+dp[v_2][1],\ dp[v_1][1]+dp[v_2][0])$
- $dp[u][1]$ :显然直接由不选绿色的儿子转移过程即可,$dp[u][1]=dp[v_1][0]+dp[v_2][0] + 1$
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
struct node {
int cnt = 0;
int son[2] = { 0,0 };
} p[N];
string s;
int tot;
int dp[N][2];
void dfs(int u) {
for (int i = 0;i < p[u].cnt;i++) {
p[u].son[i] = ++tot;
p[tot].cnt = s[tot] - '0';
dfs(tot);
}
}
int main() {
cin >> s;
int n = s.size();
s = '0' + s;
p[1].cnt = int(s[++tot] - '0');
dfs(1);
for (int i = n;i >= 1;i--) {
dp[i][1] = dp[p[i].son[0]][0] + dp[p[i].son[1]][0] + 1;
dp[i][0] = max(dp[p[i].son[0]][1] + dp[p[i].son[1]][0], dp[p[i].son[0]][0] + dp[p[i].son[1]][1]);
}
cout << max(dp[1][1], dp[1][0]) << " ";
for (int i = n;i >= 1;i--) {
dp[i][1] = dp[p[i].son[0]][0] + dp[p[i].son[1]][0] + 1;
dp[i][0] = min(dp[p[i].son[0]][1] + dp[p[i].son[1]][0], dp[p[i].son[0]][0] + dp[p[i].son[1]][1]);
}
cout << min(dp[1][1], dp[1][0]) << '\n';
return 0;
}